基于惯导辅助单星定位的卡尔曼滤波动目标定位方法与流程

本发明是一种基于惯导辅助单星定位的卡尔曼滤波动目标定位方法，特别涉及最小二乘-牛顿迭代(leastsquares-newtoniteration)、惯性导航系统(ins)辅助定位以及卡尔曼滤波(kf)融合的方法。

背景技术

现今的卫星定位技术已经趋于成熟，各大国或区域均拥有自己的卫星导航定位系统，能够为用户提供快速、高精度的定位服务。但如今的卫星导航系统均是基于卫星星座构建，利用伪距测量进行定位，要求至少四颗布局良好的卫星才能实现一次定位，是一套精密复杂的系统。也正因为它的精密复杂，所以系统本身十分脆弱，一旦关键节点卫星有所损失，就会制造出大片的定位真空区域。因此开发一种星座拒止条件下的应急卫星定位系统十分有必要。与此同时单星系统由于无需高精度原子钟和复杂系统的配合，研发生产成本低，布置方便快捷。为应对上述情况，不少大国均有相关的技术储备或实际设备投入使用，例如美国海军的transit系统，美苏法加的cospas-sarsat系统和美法建立的argos系统。

一般评价定位方法实用性的指标有三：1.定位精度、2.目标接收机复杂度、3.对卫星载荷要求。

最早期提出的单星测距测角算法测量卫星与目标之间的角度信息和距离信息，可以在空间确定唯一的位置。利用卫星与目标之间的时差确定两者的距离，但这里还要考虑钟差的影响，关键是如何同步时间，可以采用双向时间对比技术获得钟差。利用天线阵的相位差算得角度。这种方法原理简单但由于卫星距地面太远，因此对角度测量精度提出了很高的要求，目标接收机复杂度高，实现难度和成本很大。

之后又提出了伪距辅助的的径向加速度单星定位方法和相干测角的单星定位方法。其中基于伪距辅助的径向加速度单星定位要求已知卫星的星历信息，利用卫星的径向加速度测量值和伪距信息根据运动学原理构建方程组求解出目标坐标。因此径向加速度的估计精度以及卫星的星历准确度直接决定了定位精度。当径向加速度模型估计精度较低时，定位精度也会大幅下降。基于相干测角的单星定位方法中卫星的发射天线为相干天线阵列，要求预先根据方位角和俯仰角间隔一定角度条件下构建样本库，将天线阵的实测相位差信息与样本库中的数据进行相关运算，找出最大值即可得到方位角。但由于相干测角在大尺度上的精度很难提升，加上需要繁琐的样本库构建，因此实际操作难度大。

使用广泛的多普勒单星定位是利用多普勒原理测得的多普勒频移值，在已知卫星星历提供的卫星速度和卫星发射信号频率的条件下，计算出卫星飞行方向与接收机连线的夹角，采用时间换空间的策略，结合地面高度值即可解出定位目标点。对于静态目标定位精度高，对卫星载荷要求低，实用性强；但由于多普勒频移测量值易受干扰出现波动，可能会使定位结果出现一定的偏差。

后来提出的积分多普勒单星定位方法采用一段时间而非某一时刻的多普勒测量值取积分作为定位结果，很好地解决了多普勒测量值波动的问题，同时由于多普勒积分值反映的是伪距差值的大小，因此抵消了钟差的影响，对静态目标定位效果更佳。然而对于动态目标，误差仍在千米级以上。

基于波束扫描的单星定位方法对于静态目标定位精度高，使用可调整角度的高精度天线向地面投射波束，将待定位目标附近划分为多个片区，让波束轮流覆盖各个片区，将检测到卫星波束的片区中心坐标取平均得到定位点，以此为基础缩小波束半径再次扫描直至达到要求的精度。但该方法需要地面控制中心、卫星处理中心和用户终端三个部分协同工作并保持实时通信，只适合于少量静态目标的定位。

ins辅助的定位方法现今主要用于gps等星座定位系统在少于4颗观测卫星条件下的临时目标跟踪定位，但其在缺少校正的情况下存在发散的问题，实际应用有一定的局限性。目前最成熟最稳定的卫星定位信息源仍是基于伪距测量的定位，但不满足单星定位要求。

技术实现要素：

针对现有单星导航定位系统定位精度较差、定位稳定性较差、难以实现动态目标定位的问题，本发明提出一种基于惯导辅助单星定位的卡尔曼滤波动目标定位方法，主要包括最小二乘-牛顿迭代单星定位初始解算、ins惯导位移补偿和卡尔曼滤波融合反馈三个组成部分：其中最小二乘-牛顿迭代单星定位初始解算部分要求事先构建单星运行轨道以获得单星星历数据，利用测得的三个时刻的卫星相对地面定位目标伪距值，利用最小二乘方法解出目标定位初始解，使用牛顿迭代进一步逼近真实结果；其次由于目标处于运动状态，上述最小二乘需要ins惯导部分输出目标实时位移反馈给最小二乘和其后的卡尔曼滤波器对结果进行校正；最后是卡尔曼滤波部分，由于定位目标位置变化的连续性，发挥无迹卡尔曼滤波器(ukf)精度高和鲁棒性强的优势，经过定位位置迭代和融合滤波后得到目标的定位结果，能有效提高动态环境下的单星导航的定位精度并保持较长时间的稳定定位。

这种单星定位方法普适性好，对于静态和动态目标均适宜，相比于原有的单星定位方法不仅实现难度低、定位精度高，而且鲁棒性强，同时具有收敛迅速的优点，尤其适宜于特殊环境下动态目标的单星定位。

本发明的技术方案为：

所述一种基于惯导辅助单星定位的卡尔曼滤波动目标定位方法，其特征在于：包括以下步骤：

步骤1：采用积分多普勒单星定位方式获得卫星与定位目标之间的积分多普勒测量值，结合定位目标测高计获得的高度值h和卫星星历中得到的卫星各时刻坐标求出定位目标初始静态定位阶段的定位目标坐标x＝(x,y,z)；

步骤2：以步骤1得到的定位目标初始静态定位阶段的坐标x＝(x,y,z)为初始值，利用连续三个时刻卫星与定位目标间的伪距、ins惯导输入的定位目标位置偏移、卫星坐标和目标测高，联立公式

其中{ri,ri+1,ri+2}分别表示第i、第i+1和第i+2个时刻的卫星和定位目标之间的伪距，卫星在第i、第i+1和第i+2个时刻坐标分别为{xi,yi,zi}、{xi+1,yi+1,zi+1}和{xi+2,yi+2,zi+2}，定位目标在第i、第i+1和第i+2个时刻坐标分别为{xi,yi,zi}、{xi+1,yi+1,zi+1}和{xi+2,yi+2,zi+2}，{ri,x,ri,y,ri,z}、{ri+2,x,ri+2,y,ri+2,z}分别表示i时刻与i+2时刻伪距ri和ri+2各自在地心地固坐标系下x,y,z三个方向上的投影；δtu为接收机钟差；δxi,δyi,δzi和δxi+1,δyi+1,δzi+1为惯导系统记录的目标i时刻与i+1时刻间以及i+1时刻与i+2时刻间的相对位移；

将联立公式在k-1次迭代结果[xi+2,k-1,δtu,k-1]^t处泰勒展开，并略去高阶项进行线性化处理之后得到矩阵方程式为：

g·δx＝b

其中xi+2,k表示i+2时刻第k次迭代的目标坐标值，xi+2,k-1表示在第k-1次迭代时对应i+2时刻定位目标的坐标；反复进行迭代直至增量||δx||满足设定精度后停止，得到i+2时刻定位目标的三维坐标，并将此结果作为初始定位结果x；

步骤3：建立状态变量x＝[xyzvxvyvzaxayaz]^t，其中状态变量代入值x,y,z、vx,vy,vz和ax,ay,az分别为定位目标在i+2时刻坐标系中的当前位置、速度和加速度；将状态变量初始化为并将惯导系统记录的目标i时刻与i+1时刻间以及i+1时刻与i+2时刻间的相对位移δxi,δyi,δzi和δxi+1,δyi+1,δzi+1、卫星与目标在i时刻、i+1时刻和i+2时刻的伪距值，以及目标在i+2时刻的测高值代入ukf滤波器，得到i+2时刻的定位结果。

进一步的优选方案，所述一种基于惯导辅助单星定位的卡尔曼滤波动目标定位方法，其特征在于：

步骤1中，卫星运动形成测量基线，从i时刻运动到i+1时刻，形成测量基线l12，从i时刻运动到i+2时刻，形成测量基线l13；在基线l12的终端获得i时刻与i+1时刻间的积分多普勒测量值，在基线l13的终端得到i时刻与i+2时刻间的积分多普勒测量值以及定位目标的高程值h，构建两个定位双曲面和一个球面，三个曲面相交的坐标值即为定位目标初始静态定位阶段的定位目标坐标。

进一步的优选方案，所述一种基于惯导辅助单星定位的卡尔曼滤波动目标定位方法，其特征在于：

步骤1中，i时刻与i+1时刻间的积分多普勒测量值为：

i时刻与i+2时刻间的积分多普勒测量值为：

定位目标的高程方程为：

x²+y²+z²＝h²

其中xi,yi,zi代表卫星在第i时刻的坐标，xi+1,yi+1,zi+1代表卫星在第i+1时刻的坐标，xi+2,yi+2,zi+2代表卫星在第i+2时刻的坐标；

对于上述三个方程联立为方程组

转换为x^(k+1)＝x^(k)-f′(x^(k))^-1f(x^(k))进行迭代求解，其中x^(k)表示第k次迭代的定位目标坐标值，x^(k+1)表示第k+1次迭代的定位目标坐标值，f′(x)^-1表示f(x)方程组的jacobi矩阵再求其逆矩阵；经过若干次迭代之后得到定位目标坐标x加入初始定位目标集{x0i}，i＝1,2,…n；对多个时刻积累得到的定位目标集求平均值作为定位目标初始静态定位阶段的定位目标坐标

进一步的优选方案，所述一种基于惯导辅助单星定位的卡尔曼滤波动目标定位方法，其特征在于：

步骤2中，g＝[g1,g2,g3,g4]^t，g1,g2,g3,g4为g矩阵各列向量，分别如下表示：

{ri,x,k-1,ri,y,k-1,ri,z,k-1}与{ri+2,x,k-1,ri+2,y,k-1,ri+2,z,k-1}分别表示在第k-1次迭代时对应i时刻与i+2时刻计算得到的目标与卫星之间的伪距值在x,y,z三个方向上的投影，{xi+2,k-1,yi+2,k-1,zi+2,k-1}表示在第k-1次迭代时对应i+2时刻的目标坐标。

有益效果

本发明使用积分多普勒测量获得初始定位结果，积分多普勒定位能消除卫星多普勒测量的随机误差并抵消钟差；将多个时刻的静态定位结果叠加，能尽可能的抵消随机误差对定位结果的影响。对于静态目标定位精度高，并具有校准ins的效果。

本发明使用的最小二乘-牛顿迭代收敛速度快，并且与伪距测量配合已能达到相当的定位精度，具备一定的鲁棒性。

本发明使用的ukf卡尔曼滤波器与单星定位间利用状态方程的构建实现了充分结合，能够达到二阶精度；同时实时反馈定位目标结果进行修正；在ins系统的辅助下收敛稳定、鲁棒性强，定位精度较高，完全能够支持应急条件下动态目标的单星定位需要。

本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。

附图说明

本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：

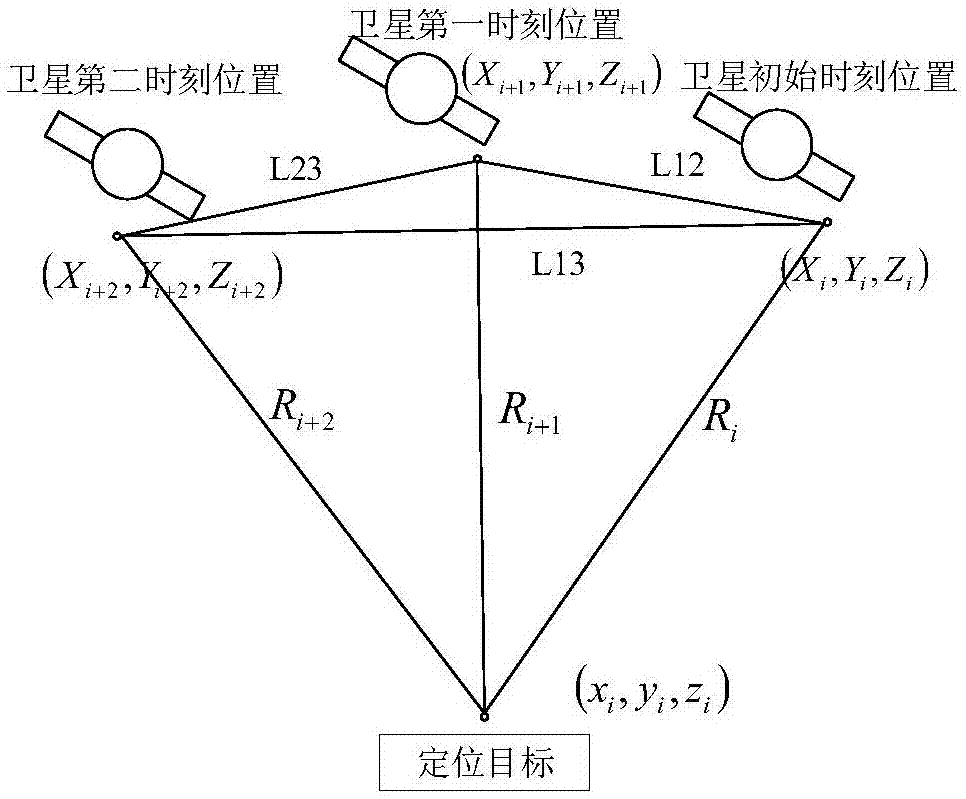
图1是基于积分多普勒单星导航定位原理说明

xi,yi,zi代表卫星在第i时刻的坐标

x,y,z代表定位目标的坐标

l12,l13,l23分别代表目标在从i时刻运动到i+1时刻、从i时刻运动到i+2时刻和从i+1时刻运动到i+2时刻的测量基线

ri,ri+1,ri+2分别对应i时刻、i+1时刻和i+2时刻卫星和定位目标之间的伪距

图2是本发明的基于惯导辅助单星定位的卡尔曼滤波动目标定位方法。

xi,yi,zi代表卫星在第i时刻的坐标

xi,yi,zi代表定位目标在第i时刻的坐标

ri,ri+1,ri+2分别对应i时刻、i+1时刻和i+2时刻卫星和定位目标之间的伪距

δxi,δyi,δzi分别对应i时刻与i+1时刻间定位目标在x,y,z三轴上的动态位移变化

δxi+1,δyi+1,δzi+1分别对应i+1时刻和i+2时刻间定位目标在x,y,z三轴上的动态位移变化

图3是本发明的单星定位方法在综合条件下的定位误差

图4是本发明的单星定位误差对比局部图

图5是本发明的单星定位误差对比整体图

具体实施方式

下面详细描述本发明的实施例，所述实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。

本发明的基于惯导辅助单星定位的卡尔曼滤波动目标定位方法结合了最小二乘算法的快速收敛性能和卡尔曼滤波器的稳定跟踪性能，使用三个时刻的卫星与目标间伪距值结合高度计获得的高度值实现目标的基础定位；并且为了保证动态环境下的单星定位精度，本发明充分利用了ins系统同时为前一级的最小二乘-牛顿迭代和后一级的卡尔曼滤波提供动态实时位移补偿，同时避免了测角侧向单星定位不稳定性，解决了现有的单星定位方法的定位精度低且鲁棒性差的问题，尤其解决了高动态目标无法进行单星定位的问题。

基本原理步骤为：

首先构建单星的卫星星历，按照设定参数设定卫星轨道以确定星历。利用积分多普勒的单星定位方式获得高精度的目标定位初始解，结合卫星星历获得高精度的基础伪距值。

定位时要想进行卡尔曼融合滤波运算就需要在每个更新时刻提供目标粗坐标，单星定位采用时间换空间的定位策略，利用定位目标三个不同时刻的伪距值和高程辅助信息，构建非线性方程组，使用最小二乘算法获得当前最优解，使用牛顿迭代方式多次重复迭代获得定位修正量补充到定位结果上进一步逼近真实值。

动态目标定位需要ins系统时刻提供目标的位移偏置，ins系统每秒输出一次目标在xyz三轴上的位移变化，在之前的最小二乘部分用于推算三个不同时刻的定位目标坐标及伪距值，与此同时之后对的卡尔曼滤波部分同样需要ins推算出的定位目标坐标。

由前面的步骤实现粗定位之后，交由卡尔曼滤波器对定位结果进行滤波处理，这里我们使用ukf滤波器，使用定位目标位置、速度、加速度构建系统状态方程，具有二阶精度。ukf卡尔曼滤波器分三部分，首先是初始化并计算测试点，其次是时间更新预测，最后经过测量更新完成一个ukf滤波周期。同时将更新之后的结果代入下一个时刻进行计算，形成反馈提高定位精度。

整个单星定位系统，由单星积分多普勒方法获得初始高精度的定位解，之后使用最小二乘-牛顿迭代的方法产生定位粗解，ukf滤波器对定位结果进行滤波稳定获得最终结果，ins系统贯穿始终，为最小二乘和ukf提供实时的位移补偿。

具体步骤如下：

1、在构建好单星运行轨迹的情况下，定位目标与卫星之间的测量数据都采用积分多普勒的方式获得。如图1所示，卫星运动形成测量基线，从i时刻运动到i+1时刻，形成测量基线l12，从i时刻运动到i+2时刻，形成测量基线l13。在基线l12的终端获得i时刻与i+1时刻间的积分多普勒测量值d12＝ri+1-ri和基线l13的终端得到i时刻与i+2时刻间的积分多普勒测量值d13＝ri+2-ri以及定位目标的高程值h，构建两个定位双曲面和一个球面，三个曲面相交的坐标值即为实际的定位结果。l12和l13积分多普勒测量值表示如下，其中x,y,z是静态定位目标坐标，xi,yi,zi代表卫星在第i时刻的坐标，xi+1,yi+1,zi+1代表卫星在第i+1时刻的坐标，xi+2,yi+2,zi+2代表卫星在第i+2时刻的坐标：

定位目标的高程方程表示如下：

x²+y²+z²＝h²(3)

其中，h是定位目标的高度信息，可以通过定位目标的高度计测量得到，卫星在各个时刻的坐标值可以通过星历得到，联合求解(1)、(2)和(3)式就可得到定位目标的坐标。联合求解三个方程需要使用牛顿迭代法，这是一个三元非线性方程组求解的问题，只需将单变量推广至方程组即可，考虑方程组

x^(k+1)＝x^(k)-f′(x^(k))^-1f(x^(k))(k＝0,1,2,...)(5)

其中x^(k)表示第k次迭代的定位目标坐标值，同理x^(k+1)表示第k+1次迭代的定位目标坐标值，f′(x)^-1表示f(x)方程组的jacobi矩阵再求其逆矩阵。经过10次迭代之后得到定位目标坐标x加入初始定位目标集{x0i}，i＝1,2,n。将多个时刻积累得到的定位目标集求平均值作为此处的初始定位目标此阶段要求定位目标处于静止状态，若不满足该条件也可直接使用伪距测量进行单星动态定位。

2、此阶段允许目标进行单星动态定位，采用时间换空间的策略，分组进行计算，每组一共需要三个时刻的卫星伪距值，解算时输出为第i+2时刻的定位结果。伪距计算公式如下：

与图2中对应，式中{ri,ri+1,ri+2}分别表示第i、第i+1和第i+2个时刻的卫星和定位目标之间的伪距，卫星在第i、第i+1和第i+2个时刻坐标分别为{xi,yi,zi}、{xi+1,yi+1,zi+1}和{xi+2,yi+2,zi+2}，定位目标在第i、第i+1和第i+2个时刻坐标分别为{xi,yi,zi}、{xi+1,yi+1,zi+1}和{xi+2,yi+2,zi+2}，δtu为接收机钟差。每组计算涉及三个时刻。惯导模块输出的两组定位目标间的坐标表达如下：

式中δxi,δyi,δzi和δxi+1,δyi+1,δzi+1为惯导系统记录的目标i时刻与i+1时刻间以及i+1时刻与i+2时刻间的相对位移，由此将式(9)(10)分别代入式(6)(8)，简化后给出动态目标和卫星间的伪距关系得：

其中{ri,x,ri,y,ri,z}、{ri+2,x,ri+2,y,ri+2,z}分别表示i时刻与i+2时刻伪距ri和ri+2各自在地心地固坐标系下x,y,z三个方向上的投影，结合气压高度计给出的i+2时刻的目标高度值如下：

此时联立方程(7)(11)(12)(13)四式，利用最小二乘解出i时刻的定位目标位置。用k表示当前时刻下正在进行的迭代次数，k-1为已完成的前一次的迭代次数，xi+2,k-1表示在第k-1次迭代时对应i+2时刻定位目标的坐标。把四个非线性方程组在k-1次迭代结果[xi+2,k-1,δtu,k-1]^t处泰勒展开，略去高阶项进行线性化处理之后得到矩阵方程式为：

g·δx＝b(14)

其中g＝[g1,g2,g3,g4]^t:

其中g1,g2,g3,g4为g矩阵各列向量，分别如下表示：

其中{ri,x,k-1,ri,y,k-1,ri,z,k-1}与{ri+2,x,k-1,ri+2,y,k-1,ri+2,z,k-1}分别表示在第k-1次迭代时对应i时刻与i+2时刻计算得到的目标与卫星之间的伪距值在x,y,z三个方向上的投影，{xi+2,k-1,yi+2,k-1,zi+2,k-1}表示在第k-1次迭代时对应i+2时刻的目标坐标。方程组g·δx＝b式中包含四个未知量，使用最小二乘法对各个时刻的动态结果联合求解，所得到的方程的解δx使得该式的左边估算量测差值与右边实际输出的测量值残差的平方和最小，此时δx为：

其中xi+2,k表示i+2时刻第k次迭代的目标坐标值，反复进行迭代直至增量||δx||满足一定精度后停止，得到第二时刻即i+2时刻定位目标的三维坐标，并将此结果作为初始定位结果x，结合ukf滤波器输出持续稳定解。

3、ins辅助定位系统承上启下，在开始阶段可以通过静态定位下精度较高的定位结果作为初始解，在最小二乘部分提供定位目标位移补偿，结合星历计算出目标的位置估测值和rx,ry,rz三轴伪距估测值。同时为下一阶段的ukf滤波器提供状态变量更新阶段的定位目标位移补偿。

4、将粗定位结果交由ukf滤波器进行处理，ukf通过无迹变换来代替传统ekf解决非线性问题。ukf滤波经过初始化之后，由循环的三部分组成，分为计算测试点、时间更新预测和测量更新：

ukf的时间预测更新需要构建状态转移矩阵φ。最小二乘-牛顿迭代部分输出的最终目标位置为x，首先进行初始化，计ukf从t＝0时刻开始：

设置系统的状态变量形式为x＝[xyzvxvyvzaxayaz]^t，同最小二乘部分类似，由于结算时我们以i+2时刻结果作为输出，ukf正式进入循环阶段时状态变量代入值x,y,z、vx,vy,vz和ax,ay,az分别为定位目标在i+2时刻坐标系中的当前位置、速度和加速度。则状态变量初始化为p0是时间预测阶段的误差先验协方差初始化矩阵，设为9×9的单位阵，我们用状态转移方程模型描述运动目标的动态过程：

其中，t时刻的状态变量先验值为t-1时刻状态变量为xt-1。由于ukf可以保证二阶精度，因此此处对状态转移矩阵φ离散化之后的估计也为两阶精度。设采样间隔为δt，其中f1f2…fn分别表示不同离散阶数对应的系数矩阵

则动态矩阵f1代表速度变化，f2代表加速度变化：

由式(23)(24)(25)得到状态转移矩阵φ为：

接下来使用状态量构建测试点，算出无迹权重系数。已知上一时刻的误差协方差矩阵为pt-1，则使用t-1时刻状态变量xt-1进行ut变换得到ξt-1，构建无迹测试点如下：

ξt-1＝[ξ⁰,ξⁱ,ξ^l+i](28)

其中ξ⁰,ξⁱ,ξ^l+i的右上角标表示对应的列向量列数，将ξ⁰,ξⁱ,ξ^l+i组合形成9×19的矩阵ξt-1，l表示状态向量维数，始终取9；对误差协方差矩阵pt-1使用cholesky分解可以得到为下三角矩阵，表示为的第i列；λ＝α²(l+κ)-l和为尺度参量，κ为次要尺度参量，取0值；α表明测试点偏离期待值的程度，取0.01。

设置t时刻先验估计值为后验估计值为单星动态定位的时间更新部分需要对生成的测试点集进行状态变换：

则xt的先验估计为：

定义运算(·)i表示括号内第i列，则表示第i列。同时定义如下的权重系数：

上式中β取值为2，此处使用i时刻、i+1时刻和i+2时刻的伪距和i+2时刻的高度值作为量测量zt：

命为一4×19的矩阵。这里的非线性变换h(·)是求得各列对应的坐标值与卫星坐标在i时刻、i+1时刻和i+2时刻的欧氏距离(实质为伪距值)以及i+2时刻各列对应的坐标值的模(实质为高度值)，此处实质为计算的各列向量在对应时刻与卫星之间的伪距值以及高度值。的组成如下所示：

(33-36)式中所有符号均为标量，δxi,δyi,δzi和δxi+1,δyi+1,δzi+1为惯导系统记录的i时刻与i+1时刻间以及i+1时刻与i+2时刻间的相对位移。此处用{xi,yi,zi}、{xi+1,yi+1,zi+1}和{xi+2,yi+2,zi+2}表示i时刻、i+1时刻和i+2时刻卫星的三维坐标值；式中各ξ的右下角标中第一位对应时刻，第二位对应三维坐标值x,y,z其中一维，第三位对应的第k列；各η的右下角标含有i的表示对应时刻，k表示的第k列，h表示计算的是高度值。分别表示向量在i时刻、i+1时刻和i+2时刻第k列的值；表示向量在i+2时刻第k列的值x,y,z值。

则zt的预测值为

先验协方差矩阵

为了使动态定位预测准确，初始化只进行一次，测量更新部分如下：

ukf滤波按照先验估计给出新的时间点下的估计值，其中状态变量的上标'∧'表示预测或校正估算值，右标′-′表示先验值，kt-1表示t-1时刻卡尔曼滤波系数矩阵，kt表示t时刻卡尔曼滤波系数矩阵，和为系统的预测协方差误差阵。同时将更新之后的结果代入下一个时刻进行计算，形成反馈提高定位精度。

性能分析

综合误差条件下本发明的单星定位仿真

本发明的单星定位仿真，采用近地点距离地表1200km的中低轨道卫星，其优势在于轨道高度较低因此多普勒积分变化明显，有利于提高定位精度。设计运行周期为2.13小时；轨道倾角为pi/6；升交点赤经为pi/3；椭圆轨道的偏心率为0.1；近地点角距为pi/6。单星定位的主要误差来源，分为定轨误差、伪距误差、卫星速度误差和ins误差等。考虑实际卫星的最大可能误差环境，设定综合误差条件为飞行时长为150秒，卫星定轨误差不超过10米，伪距误差不超过10米，卫星速度误差为0.1m/s以内，高度误差为1米以内，设定仿真总时长为3000秒单次积分时间为150秒，由于初始阶段解算原因只输出2700秒的结果。实测ins数据时采用的中精度惯性组件参数为陀螺零偏为10^-3°/h，陀螺随机游走10^-4°/sqrt(h)，初始姿态误差为2″,2″,2′，惯导初始误差为20m，运动速度为20m/s，运动方向以y轴方向为主，同时在高度方向上计入1m的测高误差。结果如图3-图5所示：

从图3观察可得基于本发明的单星定位方法在综合误差条件下虽有波动但整体平稳，无明显发散迹象。并且定位误差极值小于0.1km，均值小于0.05km，定位收敛迅速，开始输出结果10秒之后误差即收敛至小于0.1km。图中ls代表最小二乘算法，ekf代表一阶卡尔曼滤波器的算法，将这两种处理算法与本发明使用的方法在综合误差条件下进行误差绝对值(rms)比较。图4中可发现本发明的误差绝对值明显小于ekf，经100次独立重复仿真取平均值得本发明的误差均值仅为ekf多普勒方法的40.6％。图5中看出本发明与ekf的误差绝对值均远小于最小二乘多普勒单星定位方法；其中本发明误差均值仅为最小二乘的3.5％，ekf方法为最小二乘的8.6％。

尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在不脱离本发明的原理和宗旨的情况下在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。